Model building
Baseline regression model
This paper uses provincial-level panel data to study the impact of AI on GTFP. The following econometric model is constructed:
$$\:{GTFP}_{it}={a}_{0}+{a}_{1}{AI}_{it}+{a}_{j}{X}_{it}+{u}_{i}+{u}_{t}+{{\upepsilon\:}}_{it}$$
(1)
In this model, GTFPit represents the GTFP of province i in period t, AI denotes the level of AI in province i at time t, Xit are control variables that have an impact on the GTFP of province i at time t, ui indicates regional fixed effects, ut represents time fixed effects, and εit is the error term.
Furthermore, to examine the indirect channels through which AI affects GTFP, the following model is constructed:
$$\:{RIS}_{it}={a}_{0}+{a}_{1}{AI}_{it}+{a}_{j}{X}_{it}+{u}_{i}+{u}_{t}+{{\upepsilon\:}}_{it}$$
(2)
$$\:{ERN}_{it}={a}_{0}+{a}_{1}{AI}_{it}+{a}_{j}{X}_{it}+{u}_{i}+{u}_{t}+{{\upepsilon\:}}_{it}$$
(3)
In this model, RIS and ERN represent the two mediating variables of industrial structure and environmental regulation, respectively.
GMM model regression
This paper studies the impact of AI on GTFP. Since the change in GTFP is a dynamic process, the lagged value of GTFP from the previous period is included in the model for analysis. The system GMM estimation method is employed to address the potential correlation between the lagged dependent variable and the disturbance term in the dynamic panel data.
$$GTFP_{{it}} = a_{0} + a_{1} GTFP_{{it – 1}} + a_{2} AI_{{it}} + a_{j} X_{{it}} + u_{i} + u_{t} + \varepsilon _{{it}}$$
(4)
Dynamic panel threshold model
This paper refers to the research findings of Duffield, Bowers39 and constructs a threshold effect model for the impact of AI on GTFP, using technological innovation level and economic development level as threshold variables. Equation (1) is further revised as follows:
$$\begin{aligned} \:GTFP_{{it}} & = a_{0} + a_{2} AI_{{it}} \cdot I\left( {TV_{{it}} \le \:y_{1} } \right) + a_{3} AI_{{it}} \cdot I\left( {y_{1} \le \:Tv_{{it}} \le \:y_{2} } \right) \\ & + a_{n} AI_{{it}} \cdot I\left( {TV_{{it}} \ge \:y_{2} } \right) + a_{j} X_{{it}} + u_{i} + u_{t} + \epsilon _{{it}} \\ \end{aligned}$$
(5)
.
In this model, TV represents the threshold variable, I (·) denotes the indicator function, which takes the value 0 when the condition inside the parentheses is not met and 1 otherwise, and y is the threshold value.
Variable description
Explained variable
Green total factor productivity (GTFP) is the explanatory variable in this paper, and the super-efficient SBM model has become the mainstream evaluation method of GTFP because it can not only consider variable slack and non-desired outputs in the production process, but also solve the sorting problem of effective decision-making units. In this paper, based on the DEA method, using Matlab software, the desired output, non-desired output and a variety of inputs are simultaneously included in the measurement framework, and the GML indexes of 30 provinces in China are calculated on the basis of the comprehensive consideration of the non-desired output super-efficiency (SBM) model and combined with the global Malmquist productivity index. The main years of GTFP are shown in Fig. 1.
China’s GTFP in main years. (This figure is based on the standard map of the National Natural Resources Ministry’s Standard Map Service System. Http://bzdt.ch.mnr.gov.cn).
The data used are shown in Table 1. This paper adopts the research method of Wang, Xie27setting the GTFP of the base period as 1, and then multiplying it by the GML index of the following year to obtain the green total factor productivity (GTFP) for each province over a 10-year period. Due to space constraints, the exact calculation process and formulas are shown in Appendix I.
Explain variable
The core explanatory variable in this paper is AI. From the current research findings, there is no unified standard for measuring AI, and it is difficult to obtain a direct indicator of AI measurement. Therefore, this paper refers to the findings of Mhlanga40 and constructs an AI index system for each province from three dimensions: intelligent infrastructure construction, AI industry development level, and AI technology product capability, involving 8 secondary indicators, all of which are positive indicators. The entropy method is used to calculate the index weights and then build the AI index system for each province, for specific indicators, see Table 2. The AI levels of the main years are shown in Fig. 2 radar chart. Due to space constraints, the exact calculation process and formulas are shown in Appendix II.
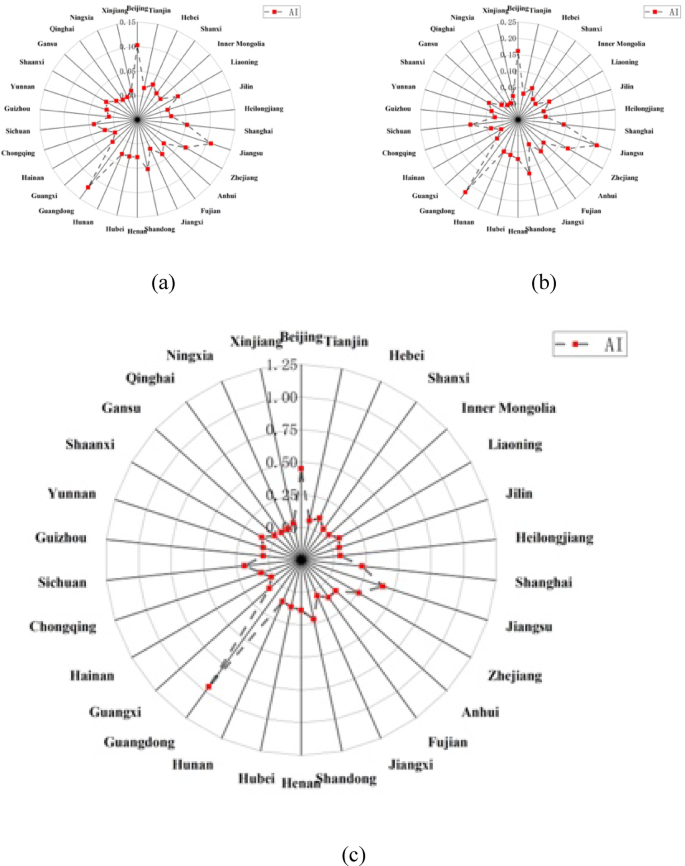
China’s AI Level in 2011 (a), 2016 (b), and 2020 (c).
Intelligent infrastructure construction. Infrastructure construction is a necessary condition for the development of AI. Without well-developed infrastructure, such as the construction of 5G, the application of Internet of Things technology, and the preparation of computer terminals, AI cannot function effectively. Therefore, fixed investment in information transmission, computer services, and software industry, the length of long-distance optical cable lines, the number of internet broadband access ports, and the number of computers at the end of the period are adopted.
AI technology product capability. The capability of AI technology products can only be widely applied when used by enterprises, promoting the development of the AI industry. Therefore, the level of AI basic research achievement transformation and the development of the AI industry itself can well represent the capability of AI technology products. Thus, in this paper, we refer to the research results of Miric, Jia41 and manually collect the number of AI patent applications in China by region to portray the level of transformation of AI basic research results, and also use the revenue of the software and information technology service industry to portray the output capacity of AI technology products.
Mediating variable
This study refers to the research results of Li, Wang42where the Industrial Structure (RIS) is represented by the ratio of the output value of the secondary industry to the GDP of each province.
For Environmental Regulation (ER), this paper synthesizes formal and informal environmental regulation indicators using the entropy method for each province. Formal environmental regulation is a composite of industrial pollution control investment completed amount/value-added of the secondary industry and environmental protection expenditure/GDP. Informal environmental regulation adopts the method proposed by Pargal and Wheeler43which includes income level, education level, population density, and age structure.
Threshold variable
The Technological Innovation Level (TI) in this study follows the methodology of De Noni and Ganzaroli44utilizing the logarithm of the annual patent grant applications per province to represent the level, encompassing invention patents, utility model patents, and design patent applications granted.
The Economic Development Level (LNAGDP) adopts the approach of Xie, Zhang45which reflects the regional economic development status through the annual per capita GDP of each province. A higher per capita GDP indicates a more advanced level of economic development.
Control variable
GTFP can be influenced by various factors. Drawing from the research outcomes of Zhang, Zhu46 and Wang, Wu47we select the following six control variables: Government intervention (GOV): This is represented by the ratio of each province’s fiscal expenditure to its GDP. Foreign direct investment (FDI): The annual actual amount of foreign investment utilized in each province serves as a proxy variable for FDI. Human capital agglomeration (HC): The level of human capital agglomeration in each province is depicted using the logarithm of the number of students enrolled at or above the undergraduate level. Marketization degree (MD): The marketization index constructed by Fan Gang and others is used as a measurement indicator.
Data source and descriptive statistics
This paper employs panel data from 30 provinces (municipalities and autonomous regions) in China for the period 2011–2020. The data sources include the “China Statistical Yearbook,” the “China Environmental Statistical Yearbook,” and the official website of the National Bureau of Statistics of China. Some data were manually collected from the China Patent Network. Additionally, this paper standardizes certain variables to facilitate analysis. Descriptive statistics for the above variables are presented in Table 3.




:max_bytes(150000):strip_icc()/GettyImages-1352028581-c7ab52907f1646fcb1def66bbf32ea4e.jpg?w=350&resize=350,220&ssl=1)



:max_bytes(150000):strip_icc()/GettyImages-1352028581-c7ab52907f1646fcb1def66bbf32ea4e.jpg?w=783&resize=783,450&ssl=1)